Group Theory in the Bedroom brings together a dozen essays written in the course of the past decade. They confront mysteries large and small. Some of the essays spring from a simple personal experience, such as trying to remember which way to flip a mattress, or driving across the Continental Divide and wondering how one would know where that landmark lies if the highway department had not put up a helpful sign. Other essays deal with events played out on a larger and more public stage: war and peace, wealth and poverty. A common thread is trying to make sense of the world we live in, and finding that ideas from mathematics and computation are useful tools.
All of the chapters in this book appeared previously as columns in magazines (one essay in The Sciences, the rest in American Scientist). They have been revised and updated, and each essay is now accompanied by an “Afterthoughts” section reviewing recent developments and, in many cases, presenting reader responses to the original publication.
The magazine columns from which the essays derive remain available online (see links below). Of course the earlier versions do not include the new material.
Table of Contents
Clock of Ages. (The Sciences, Vol. 39, No. 6, November–December 1999, pages 9–13. Online PDF.)
The Long Now group urges us to act in the best interests of posterity, but beyond a century or two I have no idea what those interests might be.... For all I know, some future generation will thank us for burning up all that noxious petroleum and curse us for exterminating the smallpox virus.
Random Resources. (American Scientist, Vol. 89, No. 4, July–August 2001, pages 300–304. Online version.)
Randomness is not something we usually look upon as a vital natural resource, to be carefully conserved lest our grandchildren run short of it. On the contrary, as a close relative of chaos, randomness seems to be all too abundant and everpresent. Everyone has a closet or a file drawer that offers an inexhaustible supply of disorder.
Follow the Money. (American Scientist, Vol. 90, No. 5, September–October 2002, pages 400–405. Online version.)
This condensation of all property in the hands of one individual is an economic catastrophe—something like the formation of a black hole in astrophysics. It’s obviously bad news for the majority of the people, who are left penniless. But even if you happen to be the big winner, your victory may prove hollow. Although you have all the riches in the world, you can’t buy a thing, because no one else has goods to sell. And you can't sell anything either, because no one has money to buy with. The whole economy is frozen.
Inventing the Genetic Code. (American Scientist, Vol. 86, No. 1, January–February 1998, pages 8–14. Online version.)
The early work on the genetic code fascinated me.... Indeed, it was hard not to feel a twinge of regret on coming to the end of the story and learning the right answer. Compared with the elegant inventions of the theorists, nature’s code seemed a bit of a kludge.
Statistics of Deadly Quarrels. (American Scientist, Vol. 90, No. 1, January–February 2002, pages 10–15. Online version.)
Warring nations bang against one another with no more plan or principle than molecules in an overheated gas.... Wars are like hurricanes or earthquakes: We can’t know in advance when or where a specific event will strike, but we do know how many to expect in the long run. We can compute the number of victims; we just can’t say who they’ll be.
Dividing the Continent. (American Scientist, Vol. 88, No. 6, November–December 2000, pages 481–485. Online version.)
It was the fourth day of a meandering coast-to-coast road trip. We were climbing through the Centennial Mountains along the Idaho-Montana border in an overloaded Toyota with a U-Haul luggage pod on the roof. As we crested Monida Pass, a sign at the roadside announced: Continental Divide, Elevation 6,823 Feet. “Well,” quipped my traveling companion, “I guess it’s all downhill from here....”
On the Teeth of Wheels. (American Scientist, Vol. 88, No. 4, July–August 2000, pages 296–300. Online version.)
For many years, the basic raw material of the computer industry was not silicon but brass. Calculators built before 1700... were all based on the meshing of metal gears.
The Easiest Hard Problem. (American Scientist, Vol. 90, No. 2, March–April 2002, pages 113–117. Online version.)
One of the cherished customs of childhood is choosing up sides for a ball game. Where I grew up, we did it this way: The two chief bullies of the neighborhood would appoint themselves captains of the opposing teams, and then they would take turns picking other players.... The aim of this ritual was to produce two evenly matched teams and, along the way, to remind each of us of our precise ranking in the neighborhood pecking order. It usually worked.
Naming Names. (American Scientist, Vol. 93, No. 1, January–February 2005, pages 6–11. Online version.)
Adam’s only chore in the Garden of Eden was naming the beasts and birds. The book of Genesis doesn’t tell us whether he found this task burdensome, but today the need to name and number things has become a major nuisance.
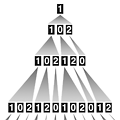
Third Base. (American Scientist, Vol. 89, No. 6, November–December 2001, pages 488–492. Online version.)
People count by 10s and machines count by 2s—that pretty much sums up the way we do arithmetic on this planet. But there are countless other ways to count. Here I want to offer three cheers for base 3, the ternary system. The numerals in this sequence—beginning 0, 1, 2, 10, 11, 12, 20, 21, 22, 100, 101, 102—are not as widely known or widely used as their decimal and binary cousins, but they have charms all their own. They are the Goldilocks choice among numbering systems: when base 2 is too small and base 10 is too big, base 3 is just right.
Identity Crisis. (American Scientist, Vol. 86, No. 6, November–December 1998, pages 508–512. Online version.)
Sometimes it’s not at all obvious whether two things are equal—or even whether they are two things. In everyday life the subtle ambiguities of identity and equality are seldom noticed because we make unconscious allowances and adjustments for them. In mathematics they cause a little more trouble, but the place where equality gets really queer is in the discrete, deterministic, and literal-minded little world of the digital computer. There, the simple act of saying that two things are “the same” can lead into surprisingly treacherous territory.
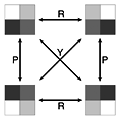
Group Theory in the Bedroom. (American Scientist, Vol. 93, No. 5, September–October 2005, pages 395–399. Online version.)
Having run out of sheep the other night, I found myself counting the ways to flip a mattress. Earlier that day I had flipped the very mattress on which I was not sleeping, and the chore had left a residue of puzzled discontent. If you’re going to bother at all with such a fussbudget bit of housekeeping, it seems like you ought to do it right, rotating the mattress to a different position each time, so as to pound down the lumps and fill in the sags on all the various surfaces. The trouble is, in the long interval between flips I always forget which way I flipped it last time. Lying awake that night, I was turning the problem over in my head, searching for a golden rule of mattress flipping.